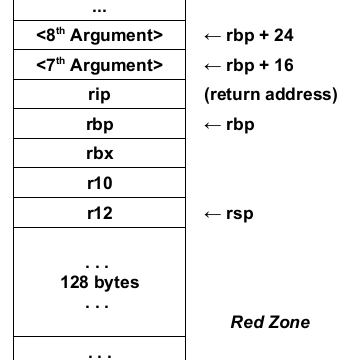
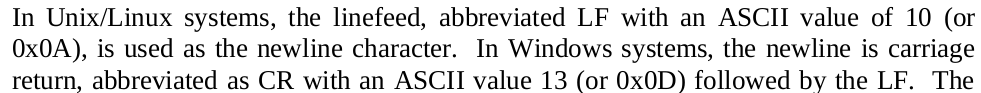PROLOGUE + EPILOGUE





LF = \n
its value must be 10

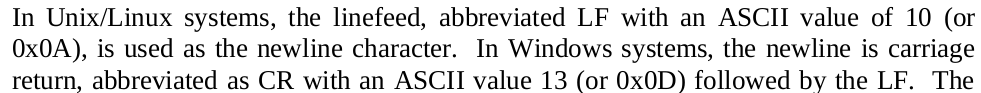
PROLOGUE + EPILOGUE







LF = \n
its value must be 10