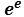
Transcendence of 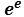
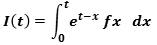 is a holomorphic function, differentiable over the complex numbers (2) in every point of its domain,
and its integrand is a polynomial of a certain degree
is a holomorphic function, differentiable over the complex numbers (2) in every point of its domain,
and its integrand is a polynomial of a certain degree 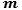 , in which the exponent of the denominator
slides all domain values [0,t]
, in which the exponent of the denominator
slides all domain values [0,t]
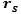 made of r=rows and s=columns
compatible with the modular form (3)
made of r=rows and s=columns
compatible with the modular form (3)
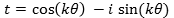 , i.e. a conjugate in polar form, with k integer.
, i.e. a conjugate in polar form, with k integer.
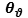 can assume, is closely related to
can assume, is closely related to
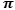 or its multiple or its fraction.
For this reason we must assume that the value of the multiple or the value of the fraction of
or its multiple or its fraction.
For this reason we must assume that the value of the multiple or the value of the fraction of 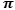 can also be non-algebraic.
can also be non-algebraic.
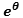 returns algebraic values, (4)
returns algebraic values, (4)
 , we get:
, we get:
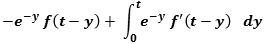 then
then 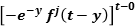 then
then 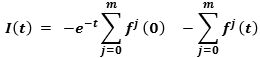
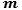 = degree of
= degree of
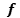 and
and 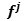 = j-th derivative of f .
= j-th derivative of f .
Let a symmetric polynomial
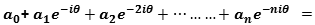
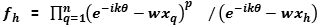
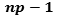 ,
with
,
with 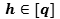 ,
, 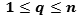 ,
, 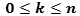 ,
and
,
and 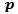 is a Prime sufficiently large.
is a Prime sufficiently large.
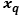 are distinct algebraic complex conjugate linearly independent.
Appropriate coefficients
are distinct algebraic complex conjugate linearly independent.
Appropriate coefficients 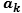 and
and 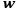 make
make 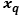 root of
root of 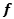
 integers non-zero , to verify the possibility of
existence of an algebraic result
integers non-zero , to verify the possibility of
existence of an algebraic result
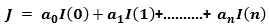 =
= 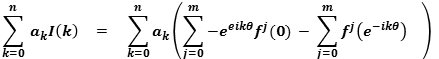 =
= 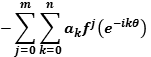 (derivative of
(derivative of 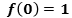 = null).
= null).
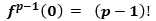 by
by 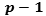 derivations, and assuming
derivations, and assuming 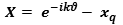 ,
we can extract from
,
we can extract from 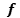 , by
, by 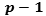 derivations, the polynomial
derivations, the polynomial 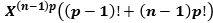 ,
then , the minimal polynomial
,
then , the minimal polynomial 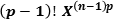 is divisible by
is divisible by 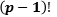 and it follows that
and it follows that 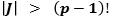
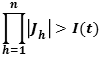 is defined in a bounded set, therefore there must be a number greater than J .
This number could be an arbitrary
is defined in a bounded set, therefore there must be a number greater than J .
This number could be an arbitrary 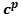 . So we have :
. So we have :
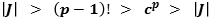
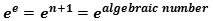
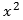 has zero in complex numbers only).
has zero in complex numbers only).