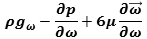written and published by Renzo Diomedi // UNDER CONSTRUCTION
3 space-dimensions cannot explane the dark matter and the dark energy.
Conventionally, we use two series of cartesian complex conjugate planes intersecting each other and on each of them.
Then we fix a point in every plane.
We name J-planes the first set of planes and
we name K-planes the set of intersecting planes.
the set of J-planes is the physical three-dimensional space made by
particles of energy imprisoned in the mass.
The set of K-planes is the electromagnetic space made by photons, particles of massless energy.
So, the K-planes intersect J-planes and vice-versa.
The distance beetween the planes is quasi null, so, the hypercube consists of two Strings intersected among themselves
Every String is composed by points (one for each plane) , the string join all the points of all the
J and K-planes vibrating in a two-dimensional surface called worldsheet,
not a 3-dimensional space
as it would be immediate to think.
Every set of planes creates a worldsheet. So the hyper cube created is composed by 4 space
dimension created by 2 worldsheets intersected.
But the fourth spatial dimension can not be perceived by our senses
created to perceive 3 dimensions only.
Considering 2 points on a sheet of paper, their distance along the surface will remain unchanged also bending the sheet,
as it will always remain the same also curving the whole book, id est the geometric variety, of which it is part.
We note that the whole universe is dotted with curved surfaces, and even when we draw a straight line on a sheet we have
to remind us that the Earth's surface is bent and that the euclidean plane considered, is valid
only by approximation locally.
If the measuring system is a Cartesian metrics, in a two-dimensional space, the axes x, y are perpendicular
to each other, but in a non-Cartesian metrics, µ, v axes are generally oblique
Length of the Strings:
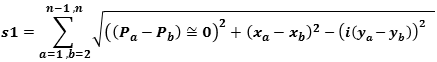
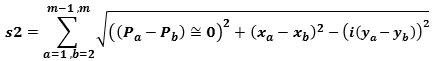
n = number of all the planes in first string , m = number of all the planes in second string ,
p = planesheet, x = Real axis , iy = Im axis
The massless electromagnetic particles and particles
with mass constitute the universe. If the distance among every point on
J-plane and every point on K-plane is zero, the massless particle intersects and coincides with particle with mass .
using the metric tensor we can calculate the sum of the vectors of coincident points of J and K :
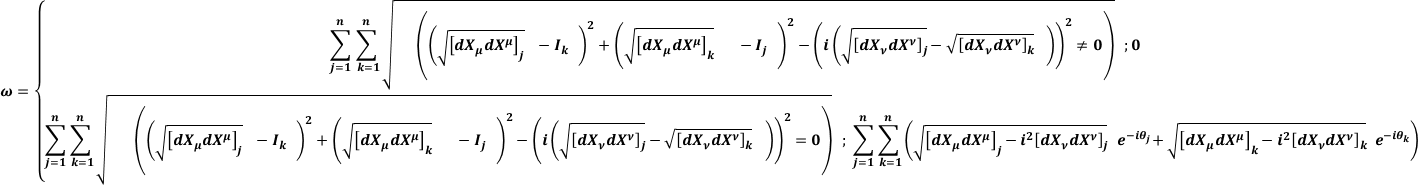
we can calcualte the distance among every point of every plane J and every point of every K:
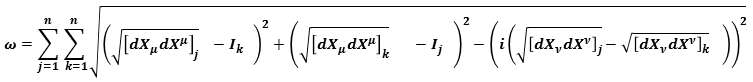
X is a generic component of the reference axes, j= series of planes , k= series of intersected planes, I = intersection point in the plane , x = Real axis , iy = Im axis
we could also consider the two sets of crossed planes as cross-cut and intersected lattices
considering the Strings belonging a worldsheet
we need to use tensors that in a geometrically bendable structure
keep equal distance beetween the lattice points
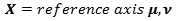
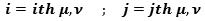
then, also using the Einstein notation
then 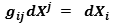
then 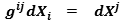
then 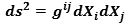
then 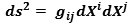
The Metric Tensor g expresses the property of a structure
geometrically curvable with the points of its lattice at a distance
always equal in relation to the structural components themselves
then 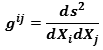 contravariant metric tensor
contravariant metric tensor
then 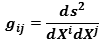 covariant metric tensor
covariant metric tensor
to be continued...........................
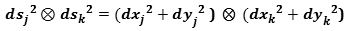
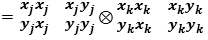
to be continued............
the series of the points of the j-planes creates a curve function that we can use as a Line Integral = 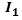
the series of the points of the k-planes creates a curve function that we can use as a Line Integral = 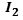
TO BE CONTINUED....................
the series of the planes J is a cube, also the series K
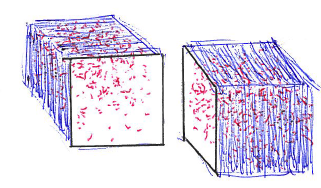
each cube composes a string that is the result of the action of so many vector fields.
Each cube, therefore, can be seen as a tensor. 2 intersecting cubes (hypercube) are a super-tensor
considering 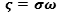 , then we have an Identity tensor:
, then we have an Identity tensor:
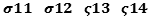
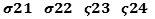
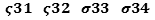
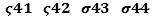
then
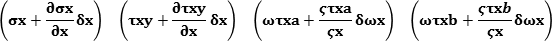
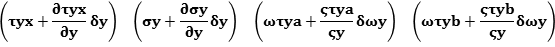
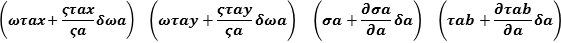
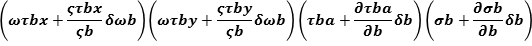
to be continued....
NS, composed by a conservative continuityequation 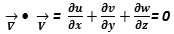 and a non-conservative
Momentum equation
and a non-conservative
Momentum equation 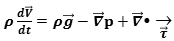 not exactly measurable as a scalar field, but divisible by
3 scalar equations laid and projected along the directions x, y, z which returned
values not coinciding.
not exactly measurable as a scalar field, but divisible by
3 scalar equations laid and projected along the directions x, y, z which returned
values not coinciding.
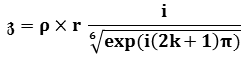 ;
; 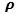 = Density ,
= Density , 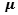 = Viscosity
= Viscosity
But the fourth space dimension could be considered as the synthesis of other 3 so in substitution of
x, y, z, so 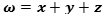 ,
, 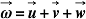 , then
, then 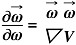 then we get a single equation in substitution of three, to get a single output
then we get a single equation in substitution of three, to get a single output 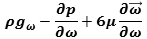
Demonstration:
Considering the 4 independent variables x,y,x,t and the 4 dependent variables u,v,w,
and p (pressure) and the 6 given by the Stress Tensor considering u, v, w components
of the shift vectors 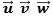 along axes x, y, z, , we have:
along axes x, y, z, , we have:
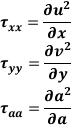
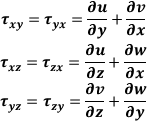
then, if the components of the viscous stress state are linearly linked
to the components of the deformation velocity through Stokes' relations,
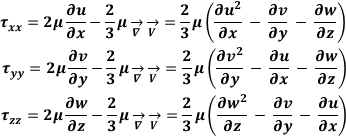
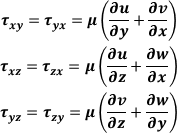
whereas 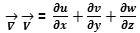
then
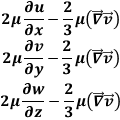
so, using 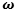 we have
we have 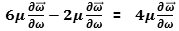
then
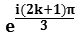
so, 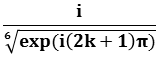
momentum scalar equations:
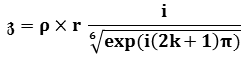
using 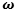 we have
we have 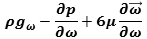
TO BE CONTINUE...
Let the Times of the series of the planes , not coinciding
TO BE CONTINUE...
(1)
co-vector , covariant plane
the axes joining the coordinates to the point, remain perpendicular at the main axes,
(but not parallel)
conventionally, indicated with lower index
contravariant plane
the axes joining the coordinates to the point, remain parallel at the
main axes (but not perpendicular)
conventionally, indicated with upper index
Home Page
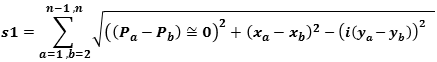
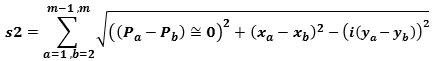
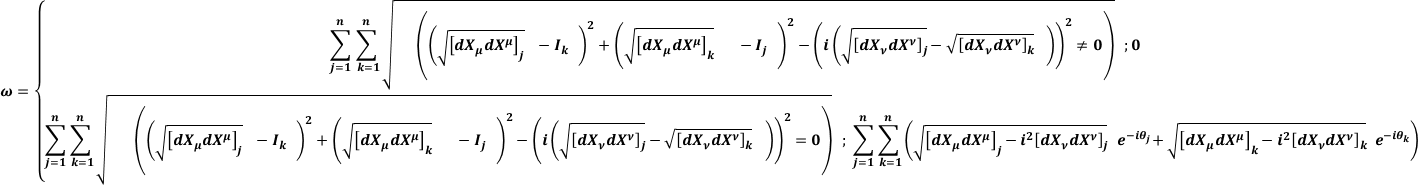
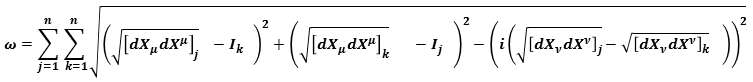
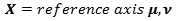
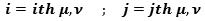

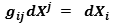
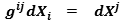
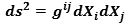
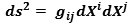
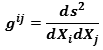 contravariant metric tensor
contravariant metric tensor
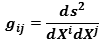 covariant metric tensor
covariant metric tensor
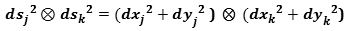
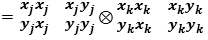
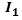
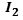

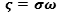 , then we have an Identity tensor:
, then we have an Identity tensor:
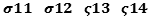
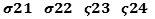
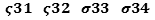
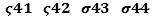
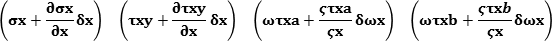
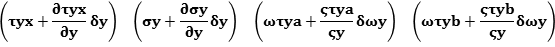
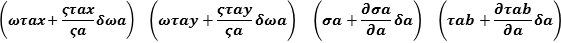
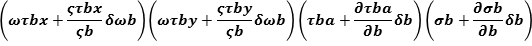
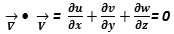 and a non-conservative
Momentum equation
and a non-conservative
Momentum equation 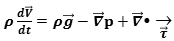 not exactly measurable as a scalar field, but divisible by
3 scalar equations laid and projected along the directions x, y, z which returned
values not coinciding.
not exactly measurable as a scalar field, but divisible by
3 scalar equations laid and projected along the directions x, y, z which returned
values not coinciding.
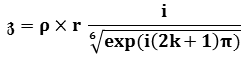 ;
;  = Density ,
= Density , 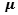 = Viscosity
= Viscosity
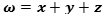 ,
, 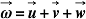 , then
, then 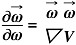 then we get a single equation in substitution of three, to get a single output
then we get a single equation in substitution of three, to get a single output 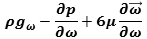
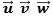 along axes x, y, z, , we have:
along axes x, y, z, , we have:
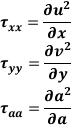
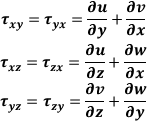
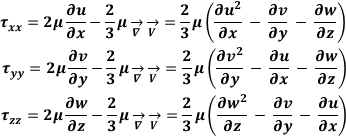
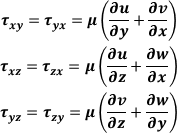
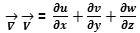
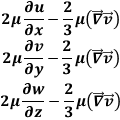
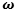 we have
we have 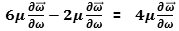
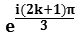
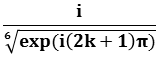
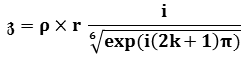
 we have
we have